How do I compute the velocity at given time?
Velocity is the rate of change of a function. And rate of change is code for take a derivative. The velocity of an object is the derivative of the position function.
You should have been given some function that models the position of the object. Take the derivative of this function. Then you can plug in the time at which you are asked to find the velocity. It really is that simple if you always keep in mind that velocity is the derivative of position.
How do I compute the acceleration at a given time?
Acceleration is the rate of change of the velocity of a function. Thus you want to take the second derivative of the position function.What if the question asks when the velocity reaches a certain value?
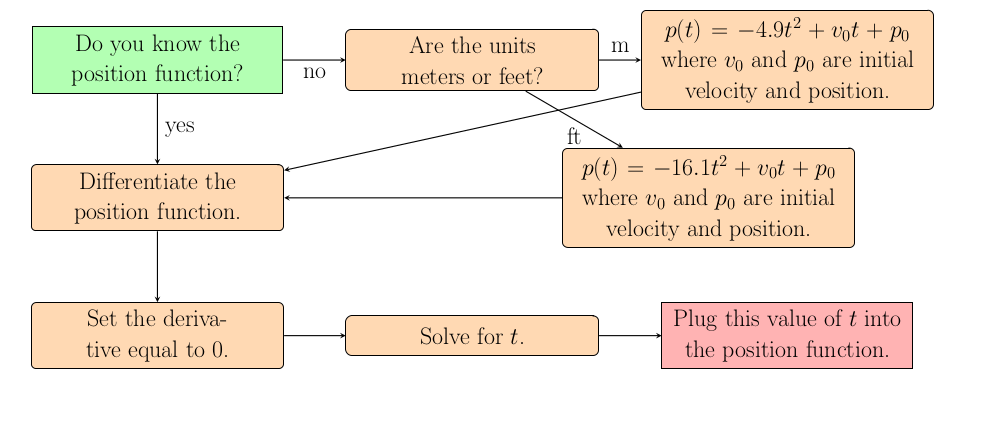
If the question asks when something occurs then we are going to need to solve for $t$. We still take the derivative of the position function, but instead of plugging in directly for $t$ we set the derivative equal to the given velocity. Then solve for $t$ and this is the time at which the velocity reaches the desired value.
Often you will be asked to determine when the velocity is 0 because this is the time at which the object changes direction. In addition an added twist could be to ask where the object is when the velocity is 0. In this case it is neccessary to solve for the time first, but then plug this time into the position function.
Can I see an example?
The most common questions involve tossing an object in the air. For these questions the acceleration will be constant so the position function will be a quadratic function and the derivative will be quite simple. For example, assume a ball's position is given by the function $p(t)=-4.9t^2+10t+2$. What is the maximum height of the ball?
At the maximum height the ball will not be rising or falling so it will have 0 velocity. Thus we need to compute $v(t)$ and set it equal to 0. Take the derivative and you should get $v(t)=p'(t)=-9.8t+10$. Thus the maximum height will occur when $t=\frac{10}{9.8}$, and if you plug this value into $p(t)=-4.9t^2+10t+2$ you will have your answer.

