What is a local maximum?
A local maximum is a point where the function is larger at that point than it is in either direction. That is, for both slightly smaller and slightly larger values of $x$ the function is smaller. From what we know about increasing and decrasing functions, this means that the function is increasing on the left of the point and decreasing to the right. We are looking for where the function switches from increasing to decreasing so we use the same intervals.How do I find Critical Points?
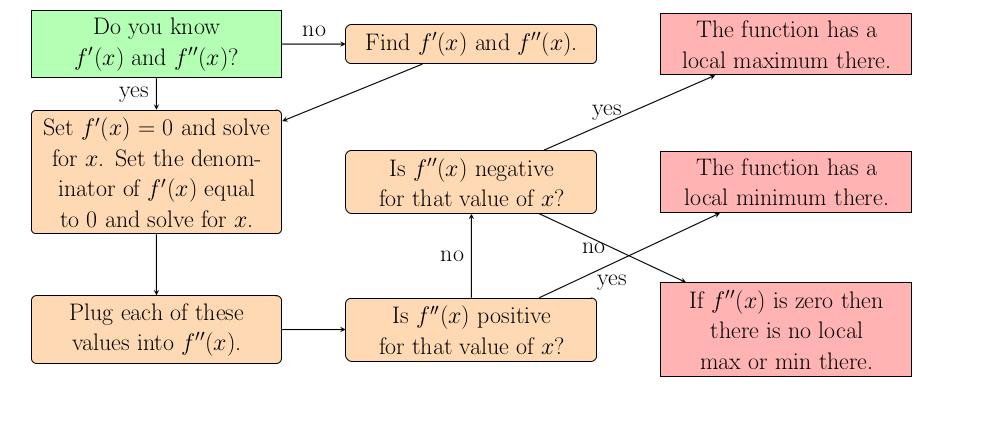
Use the same process as finding increasing and decreasing intervals. Take the derivative and then find when the derivative is 0 or undefined (denominator equals 0). Make sure to set the derivative, not the original function, equal to 0. These are the critical points that we will check for maximums and minimums in the next step.How do we know if a critical point is a local maximum or minimum?
We defined a local maximum as a point where the function switches from increasing on the left to decreasing on the right. So if we have already determined intervals of increasing and decreasing we simply look at the intervals surrounding the critical point. If they switch from increasing to decreasing then it is a local maximum. If they switch from decreasing to increasing then it is a local minimum. If the function is increasing on both sides or decreasing on both sides then the function does not have a max or min at this critical value.
If you have not already determined where the function is increasing and decreasing then you have two options. One is to determine these intervals and see where the functions switches from increaing to decreasing or vice versa. The other is the second derivative test.
If the second derivative is positive at the critical point then the function is concave up so the function has a local minimum. Of course, if the second derivative is negative then the function has a local maximum. Here positive means minimum and negative means maximum so to not be confused you should think about what concave up and down look like.
If you need to determine concavity then you will need to find the second derivative so you might as well use the second derivative test. If you are simply asked to find local maximums and minimums then you can pick either approach depending on which you are more comfortable with.
What is a global maximum?
A global maximum is simply the largest value of the function on its entire domain. A function may have many local maximums, but there can only be at most one global maximum. Since a global maximum is larger than everything it will be a local maximum so finding the global maximum is almost as easy as checking each local maximum as seeing which is the largest.
On a closed interval a function will have a global maximum, but if a function has a domain of all real numbers then it could grow larger and larger without bound and thus not have a global maximum. For instance, $f(x)=x$ has no global maximum on the domain all real numbers since the function can grow larger than any possible maximum. So we need to check the behavior of the function as $x$ approaches positive and negative infinity for any function with a domain of all real numbers.

