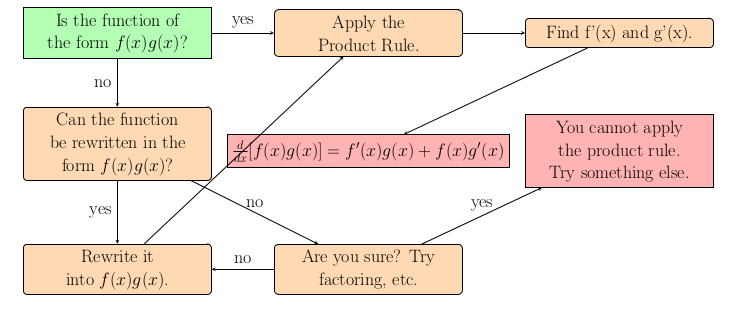
When do you use the product rule?
Use the product rule when the function consists of the product of two simpler functions. Can you identify an $f(x)$ and $g(x)$ such that the function exactly equals $f(x)g(x)$? If yes, use the product rule.
How do you use the product rule?
Once you have identified the two factors, $f(x)$ and $g(x)$, find the derivative of each factor. These derivatives could be complicated and require several steps, but they shoud be easier than differentiating the original function. Once you have carefully differentiated both factors combine the derivatives and the original functions according to the product rule: $f(x)\frac{d}{dx}[g(x)]+g(x)\frac{d}{dx}[f(x)]$.
What are some common mistakes to avoid?
Do not simply differentiate each factor and multiply the derivatives. Also you can rearrange the terms or factors according to the commutative property so your answer may come in many equivalent forms, but it is necessary that the derivatives be multiplied by the other function.


