How do we take derivatives?
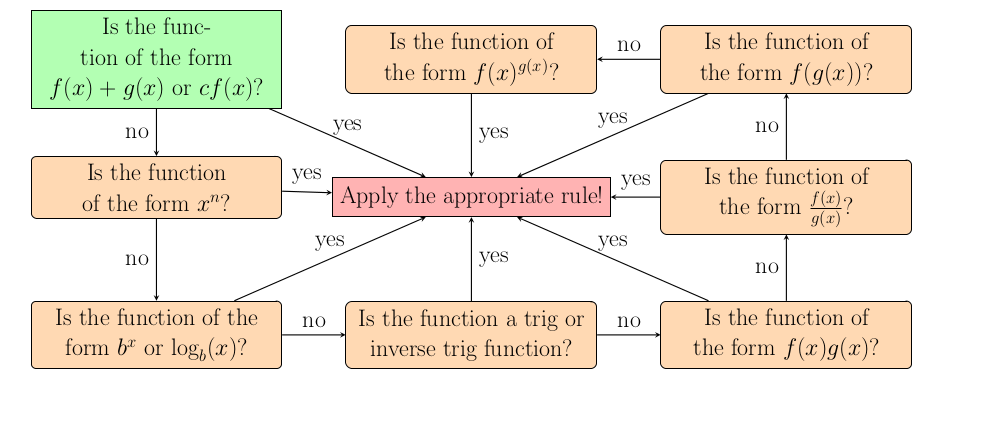
There are two important parts of differentiation that every student needs to learn. The first part is the ability to differentiate basic functions. The second part is the ability to apply four rules that allow you to break complicated functions into two simpler functions. This process is simple, but may need to be repeated multiple times and students need to be careful to keep track of exactly what they are doing.
Whenever you are asked to differentiate a function the approach is the same. First, check if you know the derivative of the function. If so you are done. If not then use the sum, product, quotient, or chain rule to simplify the function until you get to a function that you know how to differentiate. This will work every time.
What is the first step?
You need to be able to quickly differentiate a few types of functions. There are three rules to learn as well as remembering how to differentiate twelve trigonometric functions. These function are the basis of every more complicated function so it is vital that you learn how to recognize and differentiate these. The next three lessons cover
power,
exponential, logarithmic, and
trigonometric functions in depth.
What if the function is not so basic?
If the function is not so simple then we need to break it down until we reach functions that can be differentiated in the previous step. We can apply the
sum,
product,
quotient, or
chain rule to break it up. We may need to do this more than once, but in each step our goal is just to make the problem simpler. As long as we track what we are doing then we will be able to fully decompose any complex function one rule at a time.


