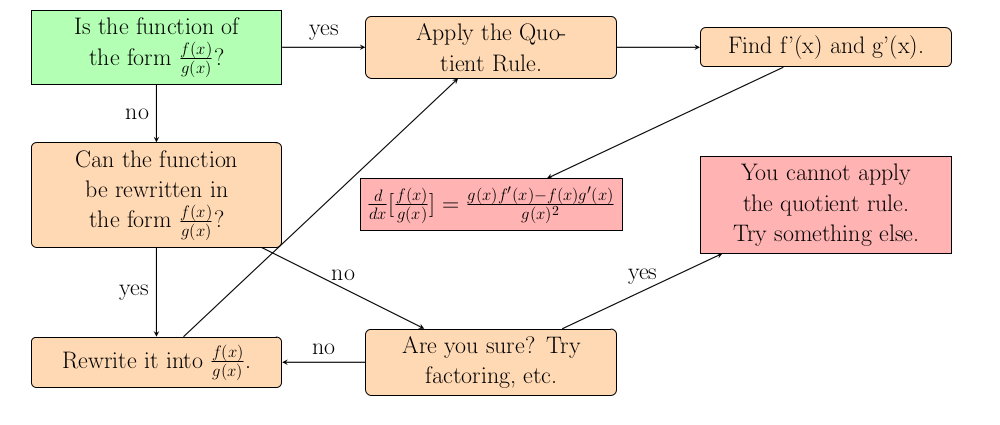
When can we apply the quotient rule?
Apply the quotient rule when the function is a fraction where the numerator and denominator both depend on $x$. The function will be of the form $\frac{f(x)}{g(x)}$ so try to identify what $f(x)$ and $g(x)$ equal. If you can break it down into that exact form then apply the quotient rule. There is no requirement that both the top and bottom must depend on $x$, but it is only really necessary in this case.
How do we differentiate a fraction?
Determine the numerator and denominator of the function. This should be easy, but make sure that you are accounting for the entire function. Then differentiate each part separately. The numerator or denominator could be extremely complicated functions so remember to treat each function carefully when differentiating. Then plug these values into the quotient rule alongside the original functions. Do not forget where the negative sign goes.
What are some common quotient rule mistakes?
The two most common mistakes are getting the negative sign switched in the numerator and forgetting to divide by the square of the denominator. The first term in the numerator must be the one with the derivative of the numerator. In the
product rule the order does not matter, but in the quotient rule the subtraction makes order matter. Make sure you memorize the exact form of the quotient rule!


