How do I calculate marginal cost?
If you do not know the cost function then you must first determine that. Then take the derivative of the cost function. This function is the marginal cost function. To find the marginal cost at a particular value, input that value into the marginal cost function. Marginal revenue works exactly the same way with the revenue function.How do I maximize profit?
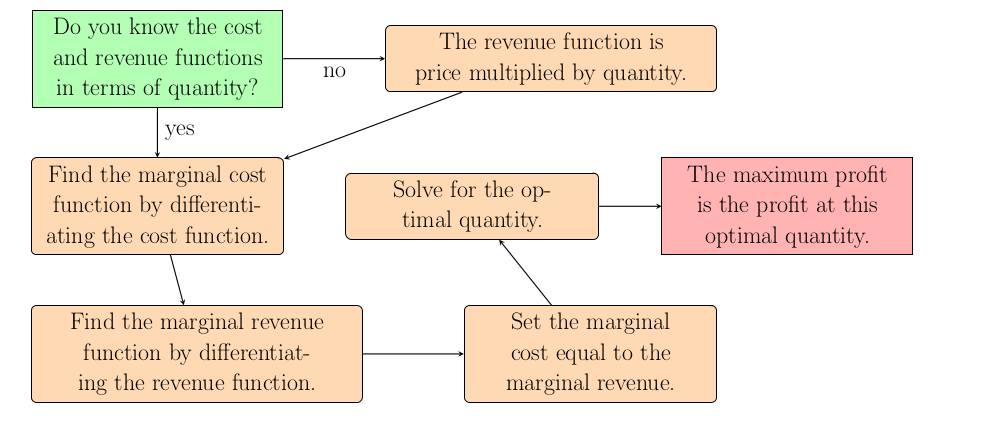
A common question in Economics is how many units to produce to create the maximum profit. If we have, or can create, formulas for cost and revenue then we can use derivatives to find this optimal quantity.
First, we need to know that profit maximization occurs when marginal cost equals marginal revenue. Producing additional units when marginal cost exceeds marginal revenue reduces profit so this intersection is important.
There are potentially five steps to consider. The first two steps are to get formulas for cost and revenue in terms of quantity. These formulas may be given or may need to be computed from supply and demand curves. Then the next two steps are to differentiate the cost and revenue functions to generate the marginal cost and marginal revenue functions. Finally set these two marginal functions equal to each other and solve for the optimal quantity. Check that the answer is actually a global maximum and make sure your answer is exactly what the question is asking for.
Can I see an example?
Your business knows that demand for its product is $q_d=1000-p$ and each additional unit costs $\$2$ to produce. What is the maximum profit that your business can achieve?
The cost function is easy to determine: $C(q)=2q$. The revenue function is the product of price times quantity sold so $R(q)=(1000-q)q$ since $p=1000-q$.
Thus the marginal cost is constant at $2$ and the marginal revenue is $-q+1000-q=1000-2q$ by the product rule.
Then we simply need to determine when $2$ equals $1000-2q$. The optimal quantity is hopefully $q=499$. And $q=499$ is a maximum by the second derivative test. However, the question asks for the optimal profit. So we must determine the profit when 499 units are produced. The cost is $2\cdot 499=998$ and the revenue is $(1000-499)\cdot 499=249999$. The profit at this quantity is the difference, which is $\$249001 $.

